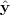i . There are a number of ways to estimate the memory matrix. One estimate of
the memory matrix W is the sum of the outer product matrices from pairs of key input and
memorized patterns
Associative memory networks include linear associative memory and Hopfield associative memory.
Linear associative memory is an effective single-layer network for the retrieval and reduction of
information. Given a key input pattern X = [x1,x2,...,xK] and the corresponding output
Y = [y1,y2,...,yK], associative memory learns the memory matrix W to map the key input xi to the
memorized output 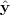i . There are a number of ways to estimate the memory matrix. One estimate of
the memory matrix W is the sum of the outer product matrices from pairs of key input and
memorized patterns
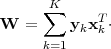 | (2.1) |
To further reduce the memorized error, an error correction approach has been introduced to minimize the error function
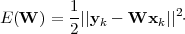 | (2.2) |
Hopfield associative memory is a nonlinear content-addressable memory for storing information in a dynamically stable environment [12]. The Hopfield network is a single-layer recurrent network which contains feedback paths from the output nodes back into their inputs. Given an input x(0), the Hopfield network iteratively updates the output vector by
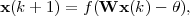 | (2.3) |
until the output vector become constant, where f(⋅) is the activation function. Associative memory is able to deduce and retrieve the memorized information from possibly incomplete or corrupted data.