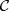 | categories,
| categories,
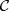 = {c1,c2,…,cj,…,c|
= {c1,c2,…,cj,…,c| |} is usually tackled as |
|} is usually tackled as |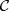 | independent binary classification problems under
{cj,cj}, for j = 1,…,|
| independent binary classification problems under
{cj,cj}, for j = 1,…,|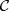 |. In this case, a classifier for
|. In this case, a classifier for 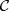 is thus actually composed of |
is thus actually composed of |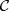 | one-against-all
binary classifiers.
| one-against-all
binary classifiers.
The concept of kernels was brought to the machine learning scenario by [9], introducing the technique
of support vector machines (SVMs). Since then there has been considerable interest in this topic
[42, 44]. Kernel methods are properly motivated theoretically and exhibit good generalization
performance on many real-life data sets. The most popular kernel methods are support
vector machines (SVMs) [54] and the recently introduced relevance vector machines (RVMs)
[53, 8]. Kernel approaches are mostly binary while certain pattern classification applications
are multi-label, multiclass problems. In this case, a problem with a set of |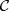 | categories,
| categories,
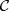 = {c1,c2,…,cj,…,c|
= {c1,c2,…,cj,…,c| |} is usually tackled as |
|} is usually tackled as |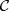 | independent binary classification problems under
{cj,cj}, for j = 1,…,|
| independent binary classification problems under
{cj,cj}, for j = 1,…,|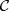 |. In this case, a classifier for
|. In this case, a classifier for 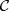 is thus actually composed of |
is thus actually composed of |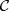 | one-against-all
binary classifiers.
| one-against-all
binary classifiers.
In the following section we will detail one of the most accepted kernel methods, namely SVMs,
treatead as a solution to a binary problem of classifying a set of data points 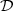 = {x1,x2,…,xi,…,x|
= {x1,x2,…,xi,…,x|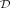 |}
into two possible target classes: {cj,cj}.
|}
into two possible target classes: {cj,cj}.
Kernel methods can be cast into a class of pattern recognition techniques in which the training data points, or at least a subset of them, are kept and used also during the prediction phase. Moreover, many linear parametric models can be transformed into an equivalent dual representation in which the predictions are based on a linear combination of a kernel function evaluated at the training data points [7]. For models which are based on fixed nonlinear feature space mapping, ϕ(x), the kernel function is given by the relation
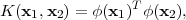 | (3.1) |
making the kernel a symmetric function of its arguments so that K(x1,x2) = K(x2,x1) [7]. The simplest example of a kernel function is the linear kernel, obtained by considering the identity mapping for the feature space in (3.1), so that ϕ(x) = x, in which case K(x1,x2) = x1T x2.
The concept of a kernel formulated as an inner product in a feature space allows us to build interesting extensions of many well known algorithms by making use of the kernel trick, also known as kernel substitution. The general idea is that, if we have an algorithm formulated in such a way that the input x enters only in the form of scalar products, then we can replace the scalar product with some other choice of kernel. For instance, the technique of kernel substitution can be applied to principal component analysis (PCA) in order to develop a nonlinear version of PCA, KPCA (kernel-PCA) [43].